1、研究的目的和意义
　　在心理、行为和其它一些社科研究领域，研究情境复杂，经常需要多个中介变量才能更清晰的解释自变量对因变量的效应。近年来，越来越多的中介研究采用多重中介(multiple mediation)模型，即存在多个中介变量的模型。不过，多数研究是将一个多重中介模型拆解为多个简单中介(即只含一个中介变量)模型，相继进行多个简单中介分析。建立结构方程模型(Structural Equation Model, SEM)进行多重中介分析，不仅可以同时处理显变量和潜变量，还可以同时分析多个自变量、多个因变量和多个中介变量的关系，是比较好的方法。近年来国际国内的主要期刊发表的中介应用研究文章，超过半数是多重中介的SEM研究，但多重中介效应的SEM分析方法的研究明显不足。本项目要研究的是至今还没有很好解决的一类前沿热点问题——多重中介效应的SEM分析方法。
　　中介变量(mediator)是除了自变量与因变量之外的重要变量，在心理学和其他社科研究领域经常碰到。如果自变量X通过某一变量M对因变量Y产生一定影响，则称M为X和Y的中介变量或M在X和Y之间起中介作用。中介作用的研究在理论上至少有以下两个重要的意义：(1) 帮助我们解释自变量和因变量关系的作用机制。(2)整合已有变量之间的关系。
　　通过开展本项目的研究，可以促进国内有关多重中介模型分析方法研究，为心理学和其他社科领域的研究人员提供强有力的多重中介模型分析工具，更好的探索和理解人类行为模式，造福社会。本课题的应用案例研究，其本身就是有实际意义的课题，设计或改编的量表、建立的模型、所得到的结论等既有示范性的方法论价值，也有具体问题的认识论价值。

2、成果的主要内容、重要观点或对策建议
2.1 结构方程模型的多重中介效应分析
2.1.1 理论分析
　　以下图所示的含有两个中介变量和的多重中介模型为例(其中的圆圈表示变量是潜变量)，此时的多重中介效应分析可以从三个角度进行，(1)特定路径的中介效应，如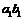、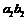和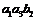，(2)总的中介效应，即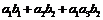，(3)对比中介效应，如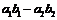、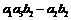和。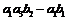

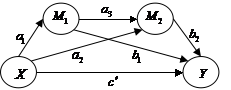
　　本项目经过文献分析，指出了目前多重中介模型分析普遍存在的问题，包括(1)分析不完整。例如，使用LISREL和AMOS软件进行多重中介分析时，只能得到总的中介效应估计值；使用MPLUS软件进行多重中介分析时，可以得到特定路径的中介效应和总的中介效应估计值，但还是得不到对比中介效应的分析结果。(2)使用Sobel检验带来的局限。在多重中介模型中，Sobel检验的局限有增无减。首先，Sobel检验统计量的推导基于正态假设，而特定中介效应、总的中介效应和对比中介效应估计值都涉及参数的乘积，因而通常都不满足正态假设，因此Sobel检验的结果是不准确的，检验力不高。其次，Sobel检验需要大样本，Sobel检验在小样本的表现并不好。第三，在多重中介模型中，Sobel检验统计量公式的分母是中介效应估计值的标准误，而这个标准误常用多元delta法计算，公式十分复杂，且需要手工计算，使用不便。建议通过增加辅助变量的方法进行完整的多重中介效应分析，使用偏差校正的Bootstrap方法进行中介检验。
总结出一个多重中介SEM分析流程，即(1)确定多重中介模型；(2)设置辅助变量；(3)偏差校正Bootstrap的SEM分析。并有示例和相应的MPLUS和LISREL程序。

2.1.2 模拟分析
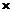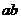　　本项目用5个因变量指标(偏差、相对均方误、统计功效、第Ⅰ类错误率、95%置信区间宽度)和5(样本容量)8(组合)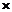2(估计方法)的实验设计对Bootstrap法和Bayesian法在多重中介效应模型(见上图)中的表现进行Monte Carlo模拟比较。结果表明，在多重中介效应分析中，当有先验信息时，推荐使用有先验信息的Bayesian方法进行中介效应分析；当先验信息不可得时，推荐使用偏差校正的Bootstrap方法进行中介效应分析。

2.1.3 应用案例分析
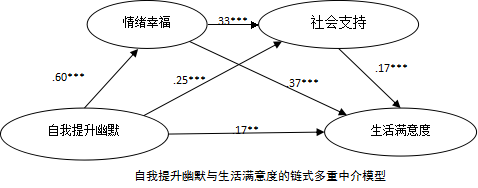
　　采用幽默风格问卷中的自我提升幽默维度、主观幸福感量表中的积极情绪和消极情绪维度、多维领悟社会支持量表和生活满意度量表对884名大学生进行调查。构建结构方程模型(见下图)，Bootstrap检验表明了多重中介效应显著，总中介效果量为63.6%，其中通过情绪幸福这一中介路径的中介效果量最大，达47.3%。未来研究可探讨在个体主义文化背景下的不同链式中介效应。

2.2 结构方程模型的多层中介效应分析
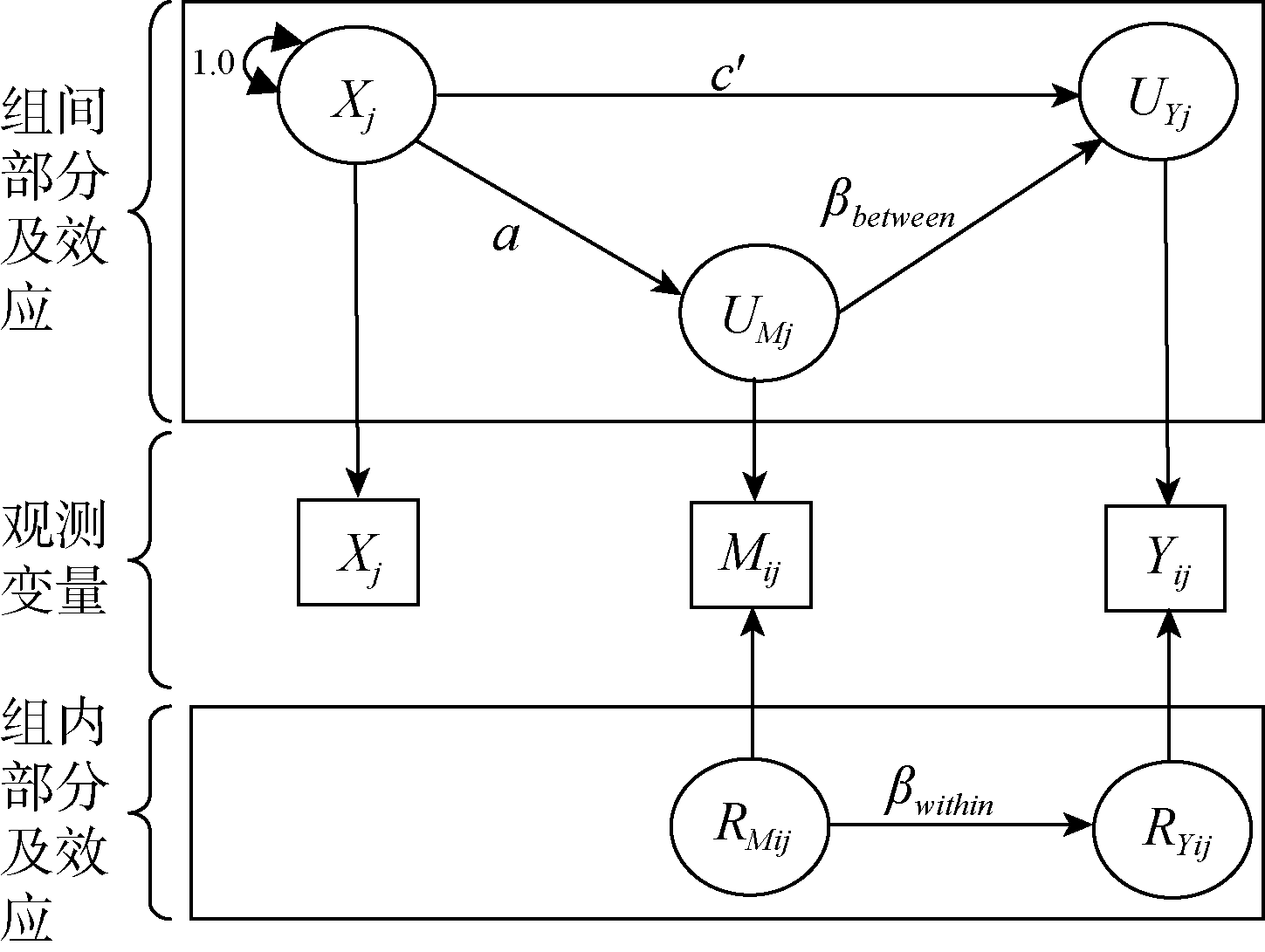
　　近年社科领域常见使用多层线性模型进行多层中介研究。尽管多层线性模型区分了多层中介的组间和组内效应，仍然存在抽样误差和测量误差。比较好的方法是，将多层线性模型整合到结构方程模型中，在多层结构方程模型框架下设置潜变量和多指标，可有效校正抽样误差和测量误差、得到比较准确的中介效应值，还能适用于更多种类的多层中介分析并提供模型的拟合指数。在介绍新方法后，总结出一套多层中介的分析流程，通过一个例子来演示如何用MPLUS软件进行多层中介分析。最后展望了多层结构方程和多层中介研究的拓展方向。

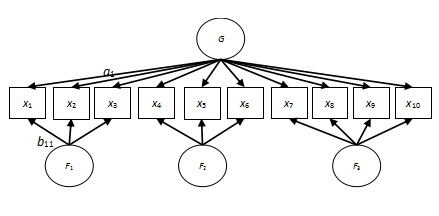
2.3 结构方程模型的新进展：双因子模型
　　双因子模型是一种既有全局因子(G)又有局部因子(F1、F2、F3)的模型(见下图)，近年来有了许多应用。本文讨论了双因子模型和高阶因子模型在数学模型、参数之间的关系，概念上和应用上的差异；概述了双因子模型在信度研究、平衡量表、探索性因子分析和项目反应理论中的应用。作为例子，在Rosenberg自尊量表结构的研究中，通过双因子模型分析了自尊特质效应与项目表述方法效应。

2.4 中介效应分析的其他研究
2.4.1 有调节的中介效应分析
　　有调节的中介模型是中介过程受到调节变量影响的模型。评介了基于Bootstrap不对称置信区间和Bayesian不对称可靠区间进行有调节的中介模型检验的三种方法，包括亚组分析法、差异分析法和系数乘积法。模拟研究发现，偏差校正的百分位Bootstrap置信区间和无先验信息的Bayesian可靠区间在有调节的中介模型检验中表现相当，都优于百分位Bootstrap置信区间的表现。建议使用系数乘积法进行第一阶段或第二阶段被调节的中介模型检验，使用差异分析法进行两阶段被调节的中介模型检验，并用一个实际例子演示如何用不对称区间估计检验有调节的中介模型。随后评述了三种有调节的中介模型检验方法在国内心理学的应用现状，并展望了检验的拓展方向。

2.4.2 类别变量的中介效应分析
　　在心理学和其他社科研究领域，研究者能熟练地进行连续变量的中介效应分析，但面对自变量、中介变量或(和)因变量为类别变量的中介效应分析，研究者往往束手无策。在阐述类别自变量中介分析方法的基础上，我们建议使用整体和相对中介相结合的类别自变量中介分析方法，并给出了分析流程。以二分因变量为例，讨论了中介变量或(和)因变量为类别变量的中介分析方法的发展过程(即尺度统一的过程)，建议通过检验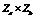的显著性来判断中介效应的显著性。用二个实际例子演示如何进行类别变量的中介效应分析。最后展望了类别变量的中介效应分析研究的拓展方向。
    （本文作者：方杰  广东财经大学副教授）